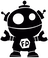Для кого эта статья:
- Студенты и школьники, изучающие геометрию
- Преподаватели математики
- Люди, интересующиеся объемом и свойствами геометрических фигур
Что такое пирамида и из чего она состоит
Пирамида — это многогранник, состоящий из многоугольника в основании и треугольников по бокам, которые образованы при соединении точки вершины фигуры и вершин её основания.
Те треугольники по бокам — это боковые грани пирамиды, а их общие стороны — её рёбра. Кроме того, у каждой пирамиды есть апофема — это перпендикулярная прямая, которая опущена из её вершины к стороне основания.
Высота пирамиды — это перпендикуляр, опущенный из её вершины к основанию.
В отличие от других многоугольников, у пирамиды нет диагоналей. Всё потому, что каждая вершина её основания соединена с вершиной самой фигуры и образует треугольную грань. Выходит, у пирамиды нет противоположных вершин. Зато они есть у самого основания, а значит, есть и диагонали этого основания.

Какими бывают пирамиды
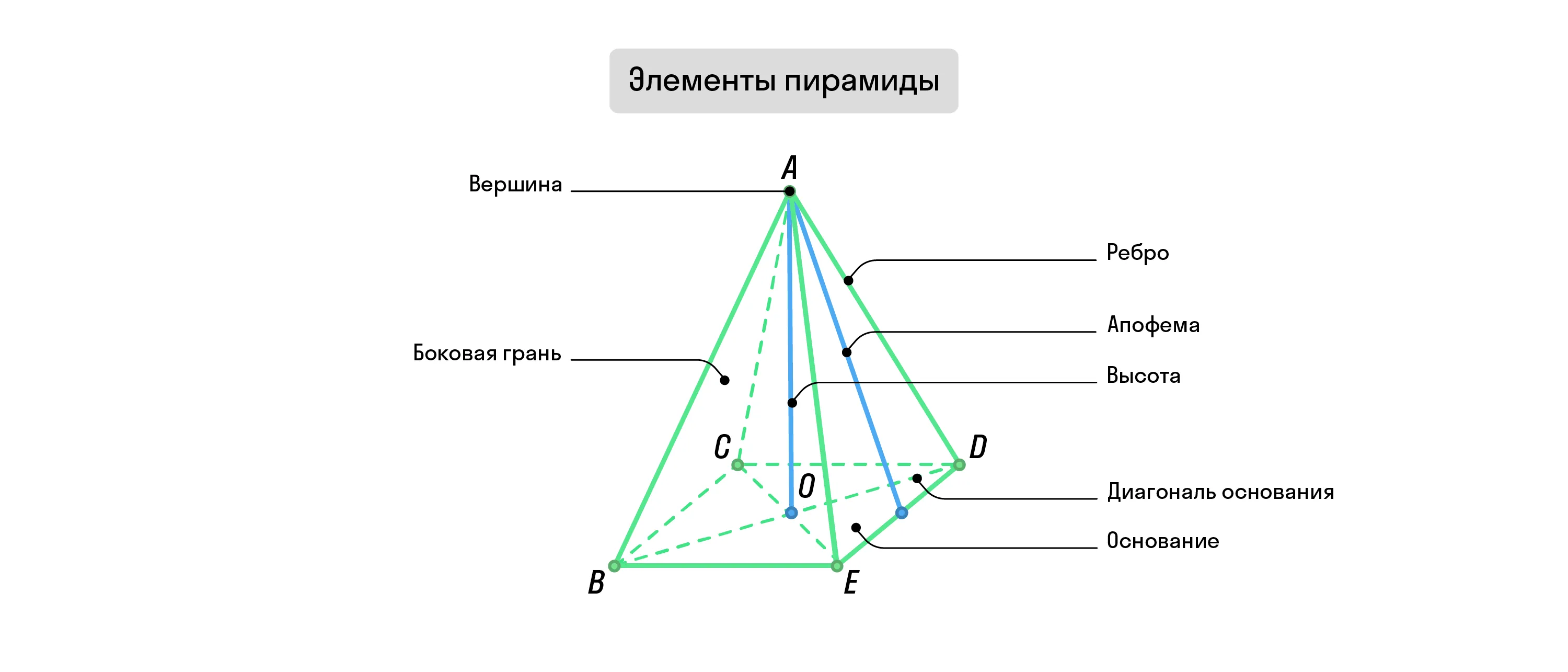
Т. к. основанием пирамиды может быть любой многоугольник, от этого зависит и тип самой фигуры. Если в её основании лежит треугольник, она будет называться треугольной. В зависимости от основания, пирамиды бывают также четырёхугольными, пятиугольными, шестиугольными и т. д.
Если в задаче неизвестно, какой именно многоугольник лежит в основании пирамиды или это не важно, условие назовёт такую пирамиду n-угольной.
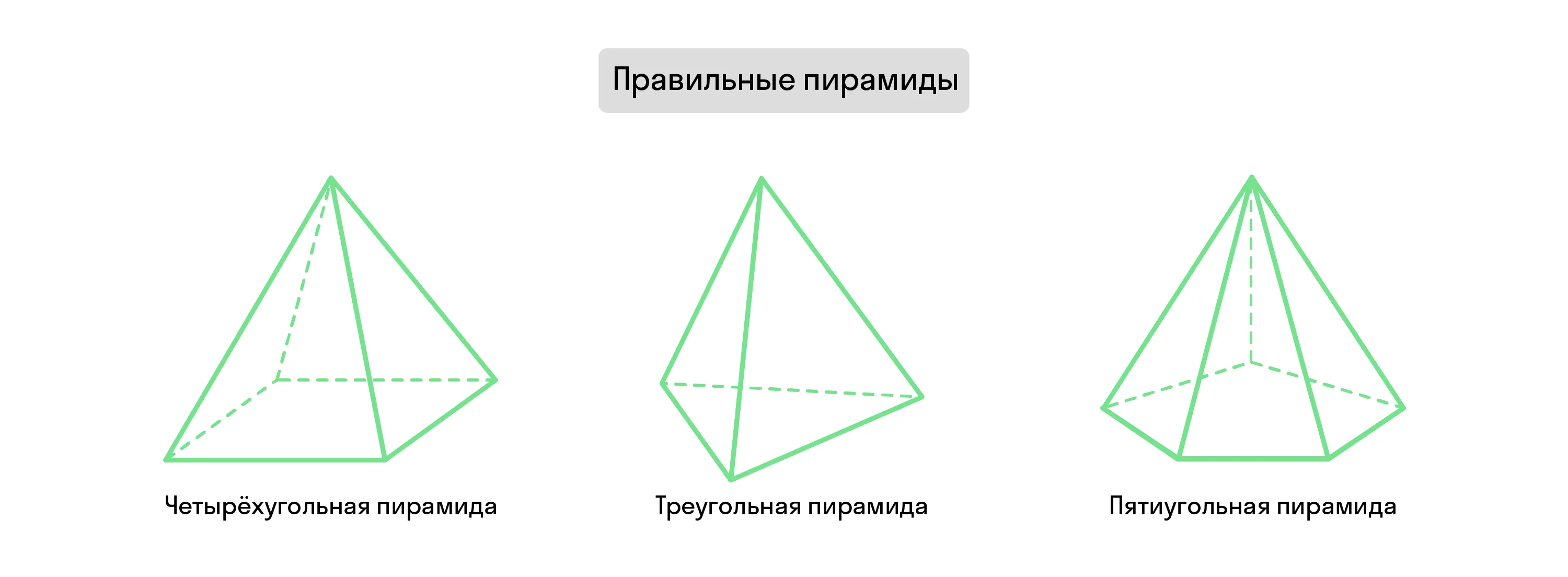
Остроугольные и тупоугольные пирамиды
Пирамида может быть остроугольной и тупоугольной. В первом случае апофема больше длины стороны основания, во втором — меньше.
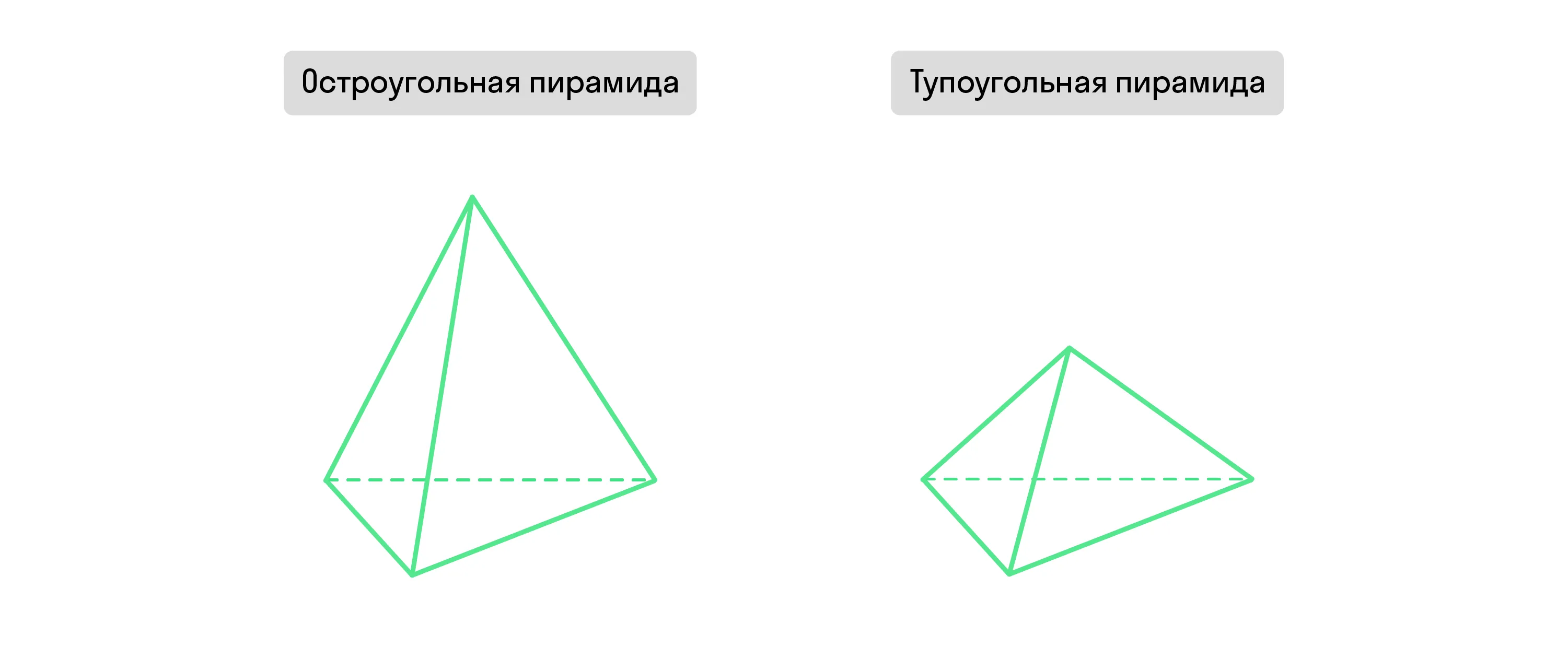
Правильные и неправильные пирамиды
Если высота пирамиды соединяет её вершину с центром основания, а оно само представляет из себя правильный многоугольник, то и пирамида называется правильной.
Все боковые грани такой фигуры — это одинаковые равнобедренные треугольники. При этом диагонали основания правильной пирамиды пересекаются в его центре и делятся им же пополам. Именно в эту точку опускается и высота этой фигуры.
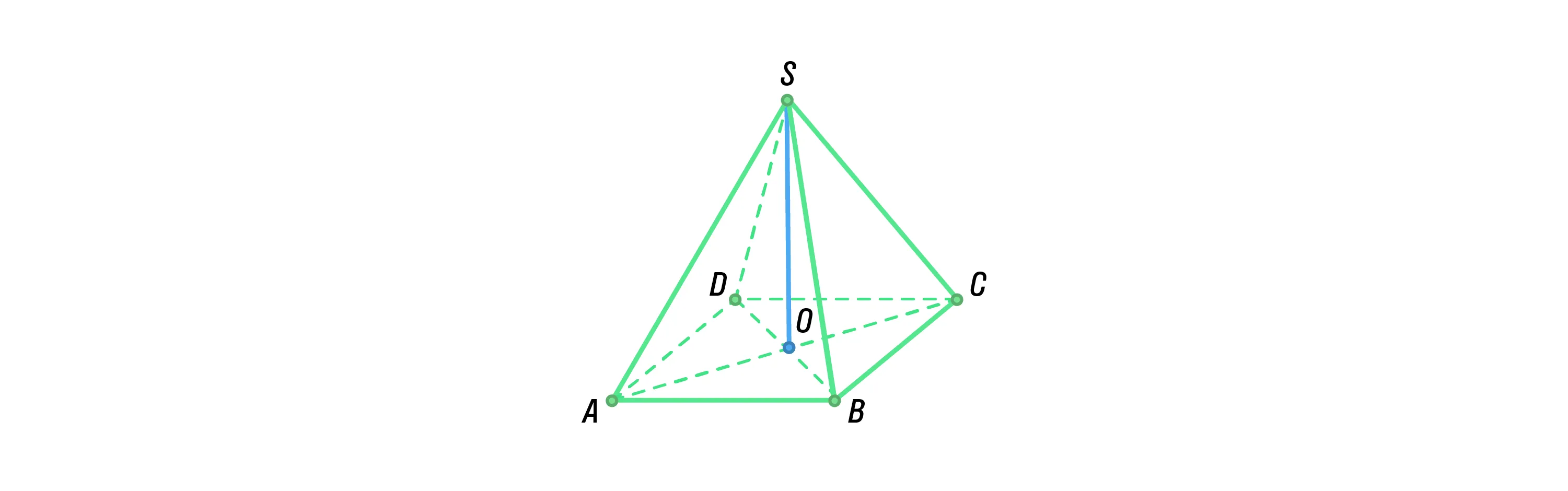
Одно из важных свойств правильной пирамиды заключается в том, что все её рёбра наклонены к её основанию под одинаковыми углами. При этом равны также длины этих рёбер и апофемы пирамиды.
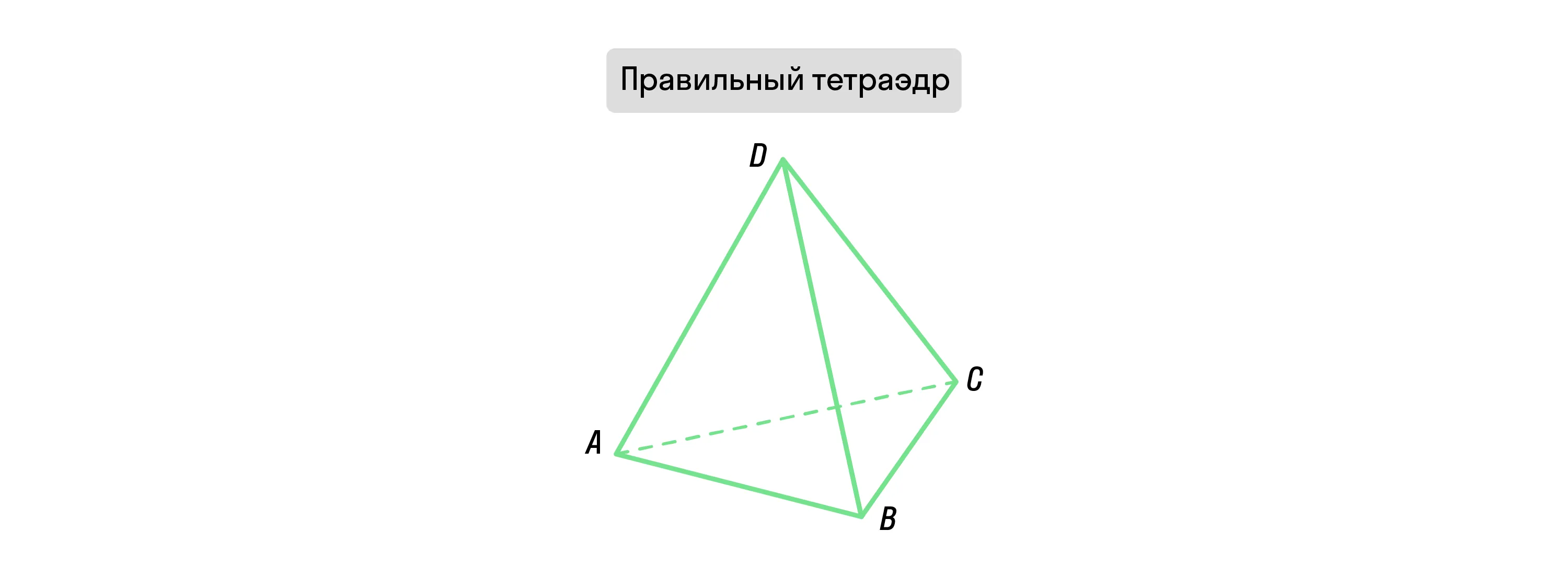
Правильный тетраэдр — это пирамида, все грани которой являются равносторонними треугольниками.
Все рёбра, грани, а также периметры и площади всех граней такой фигуры равны между собой.
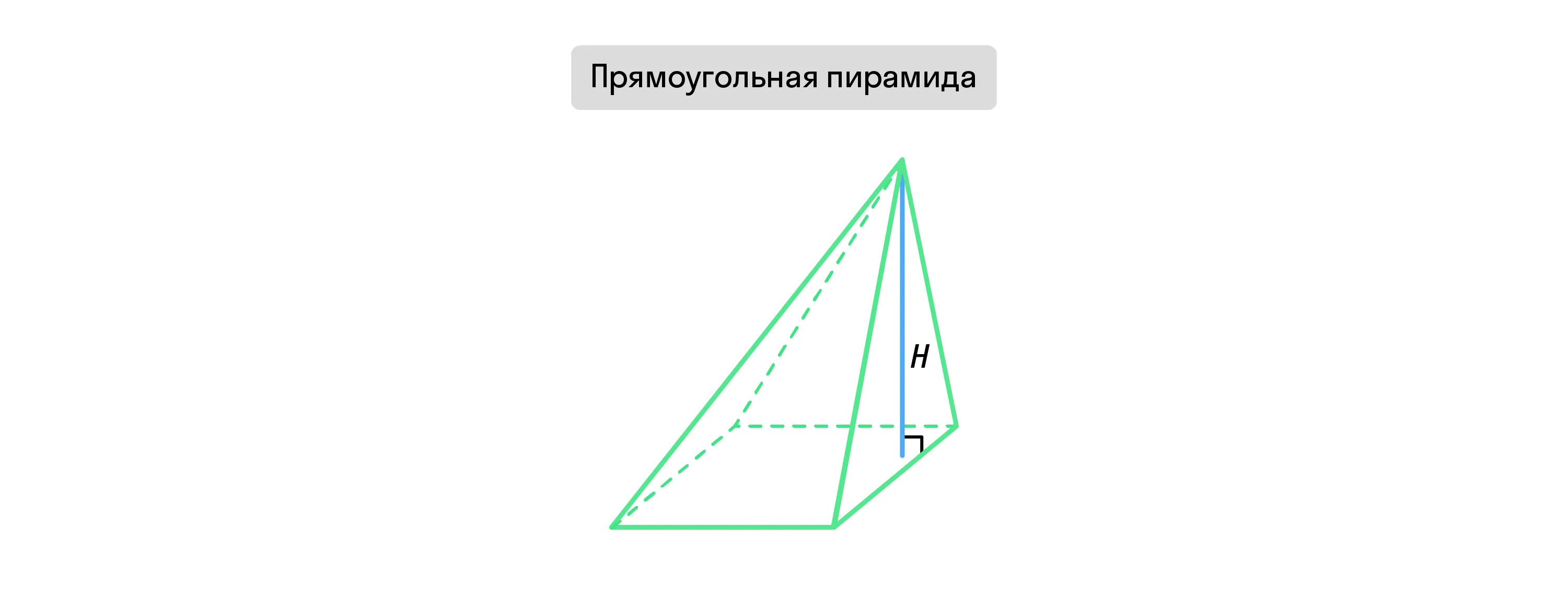
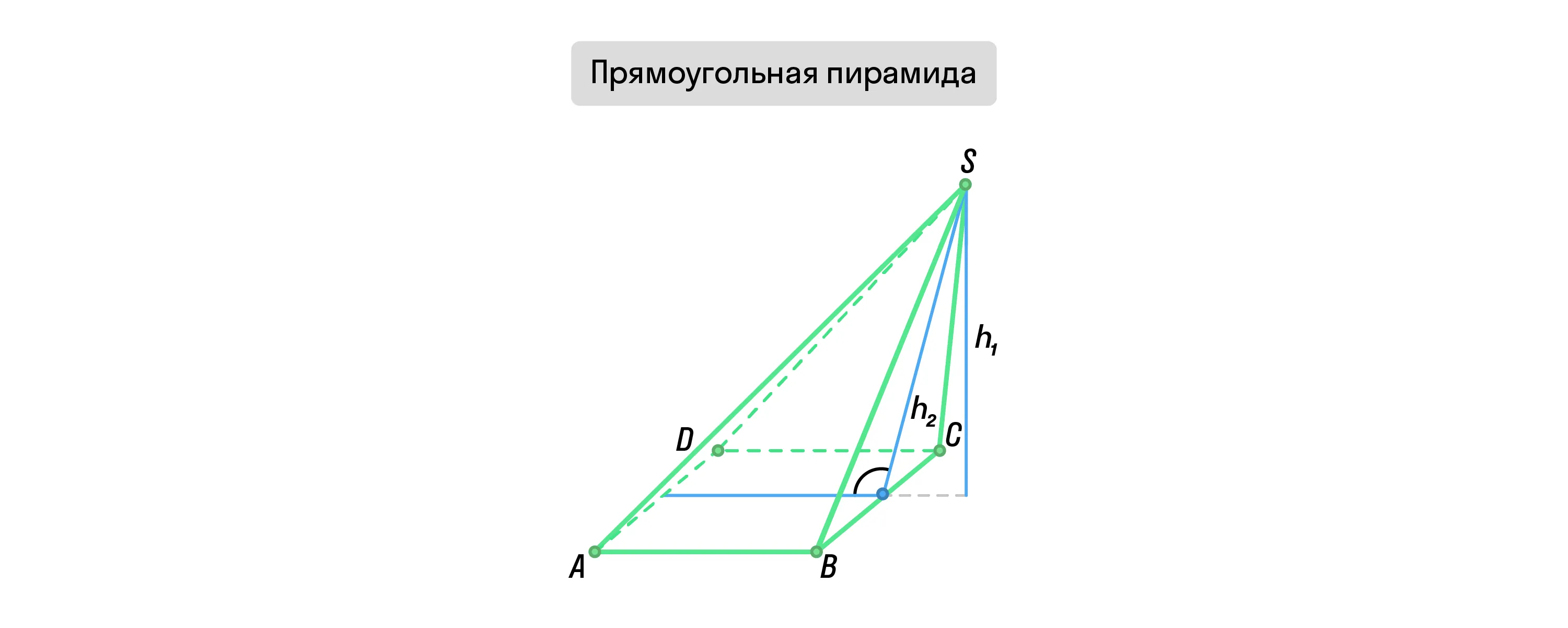
Прямоугольная пирамида
Прямоугольная пирамида — это такая пирамида, в которой одна из боковых граней перпендикулярна основанию фигуры.
У прямоугольной пирамиды проведённая высота принадлежит одной из граней. Она также равна по длине апофеме, проведённой по этой же грани.
Наклонная пирамида
Наклонная пирамида — это такая пирамида, в которой одно из рёбер образует тупой угол с основанием.
Если провести высоту такой пирамиды, она будет опущена вне основания фигуры.
Усечённая пирамида
Усечённая пирамида — это нижняя часть пирамиды, которую разделяет плоскость, параллельная основанию фигуры.
Образовавшиеся так параллельные грани усечённой пирамиды считаются её основаниями. Расстояние между ними, т. е. перпендикулярная прямая, которая опущена от одного основания к другому, — это высота такой пирамиды.
В отличие от остальных видов пирамид, у усёченной есть диагонали.
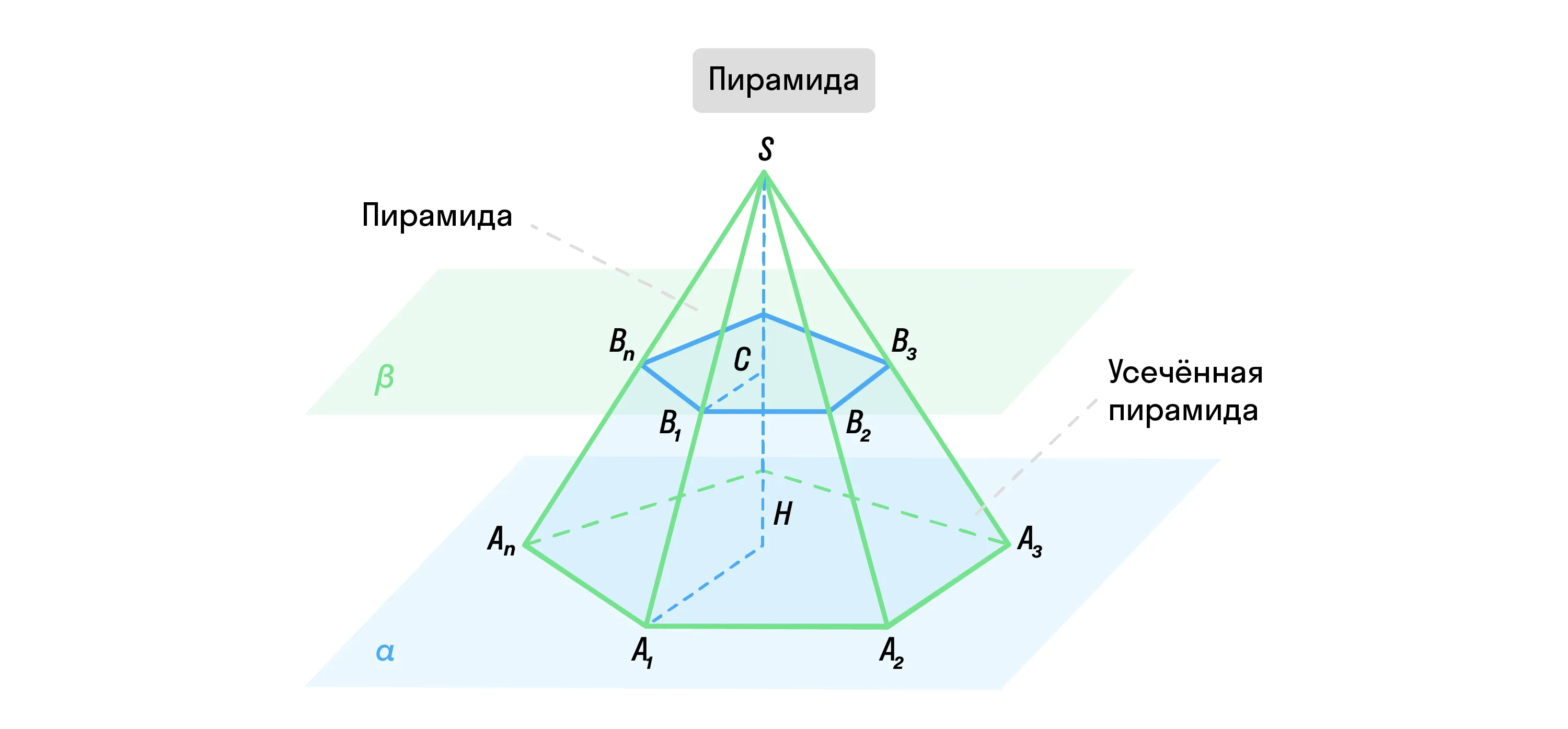
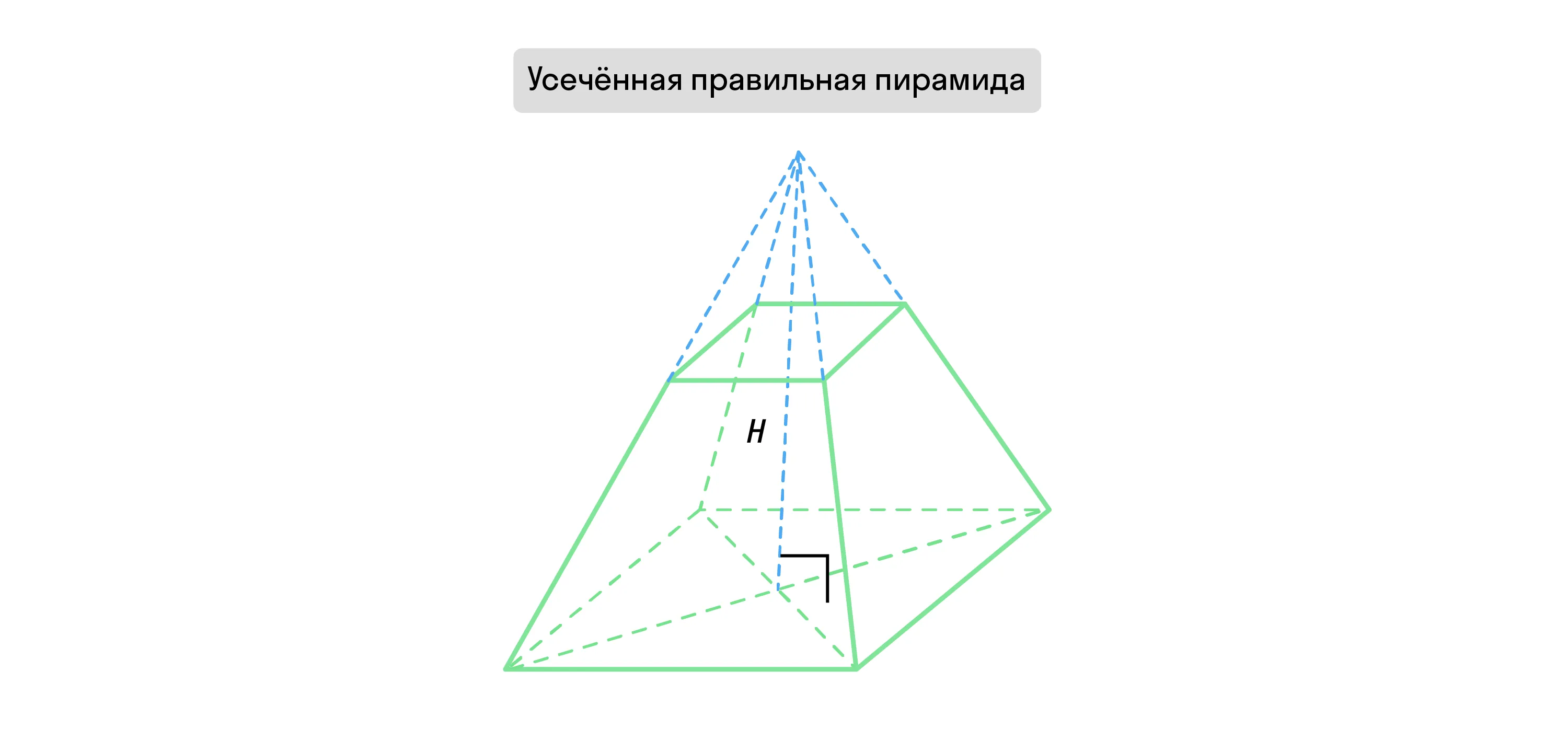
Если такая фигура была получена усечением правильной пирамиды, она называется усечённой правильной пирамидой.
Все боковые грани этой фигуры — это равнобедренные трапеции.
Пирамида и сфера
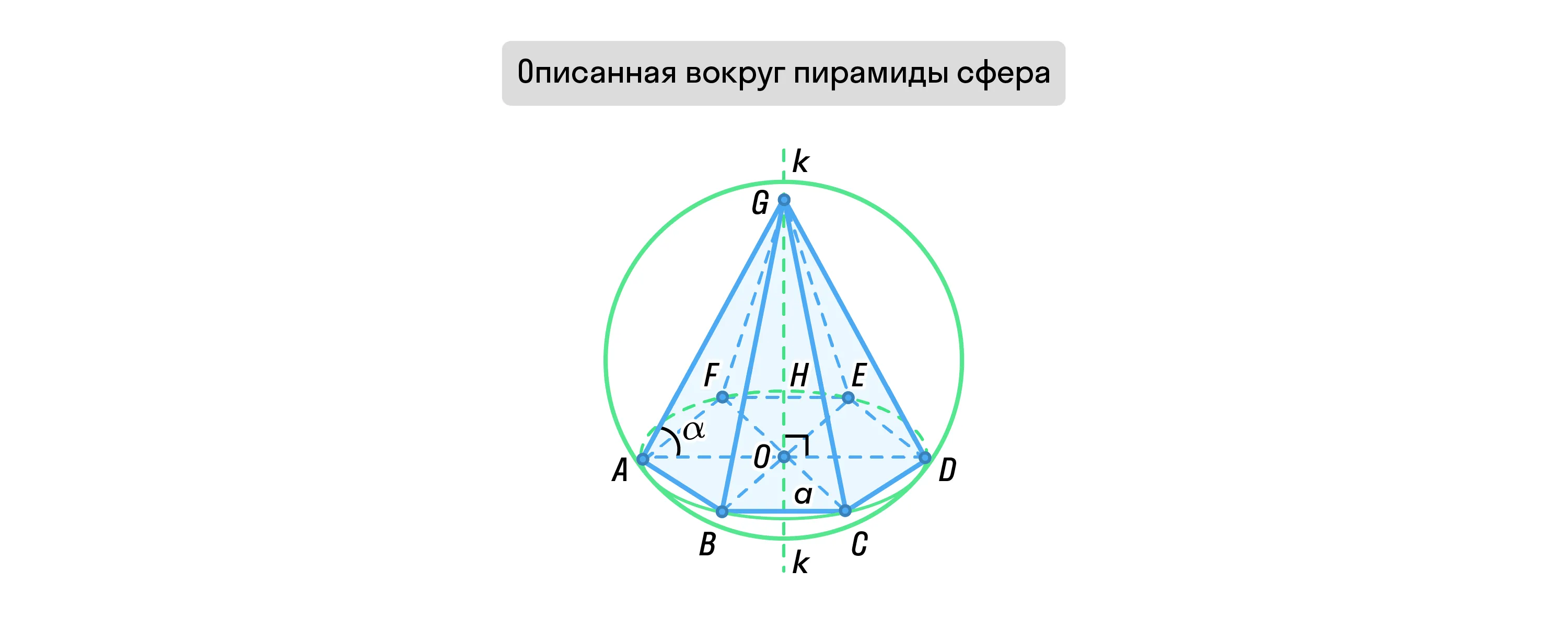
Вокруг пирамиды можно описать сферу, если в основании этой пирамиды лежит многогранник, вокруг которого можно описать окружность. Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых рёбер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
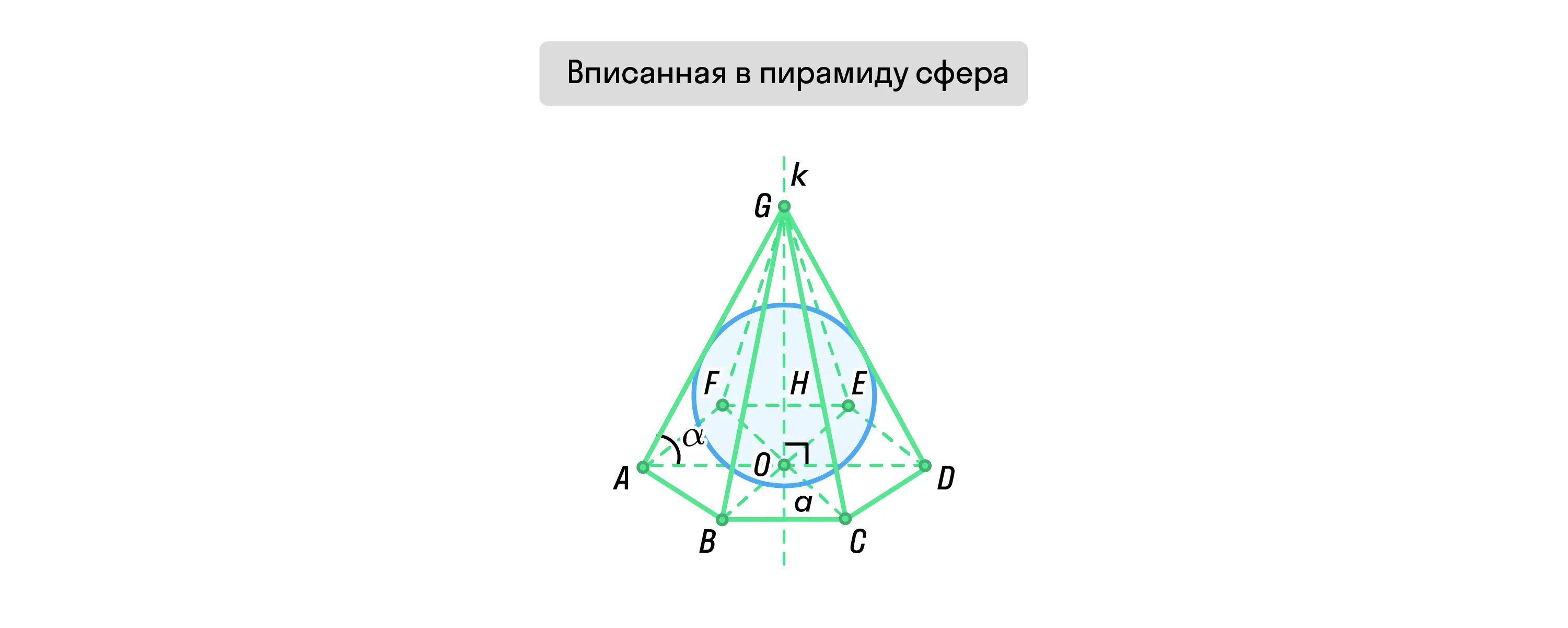
Биссекторная плоскость — это такая плоскость, которая выходит из ребра двугранного угла, которая делит его на два равных двугранных угла.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке. Эта точка и будет центром сферы.

Круглые телаЧитать →
Пирамида и конус
Если все боковые рёбра равны, т. е. перед нами правильная пирамида, то вокруг её основания можно описать окружность. При этом центр основания будет совпадать с центром этой окружности. Также перпендикуляр, опущенный из вершины, в этом случае будет проходить через центр основания. Это одно из условий, по которому пирамиду можно вписать в конус.
Второе условие — вершины конуса и пирамиды должны совпадать.
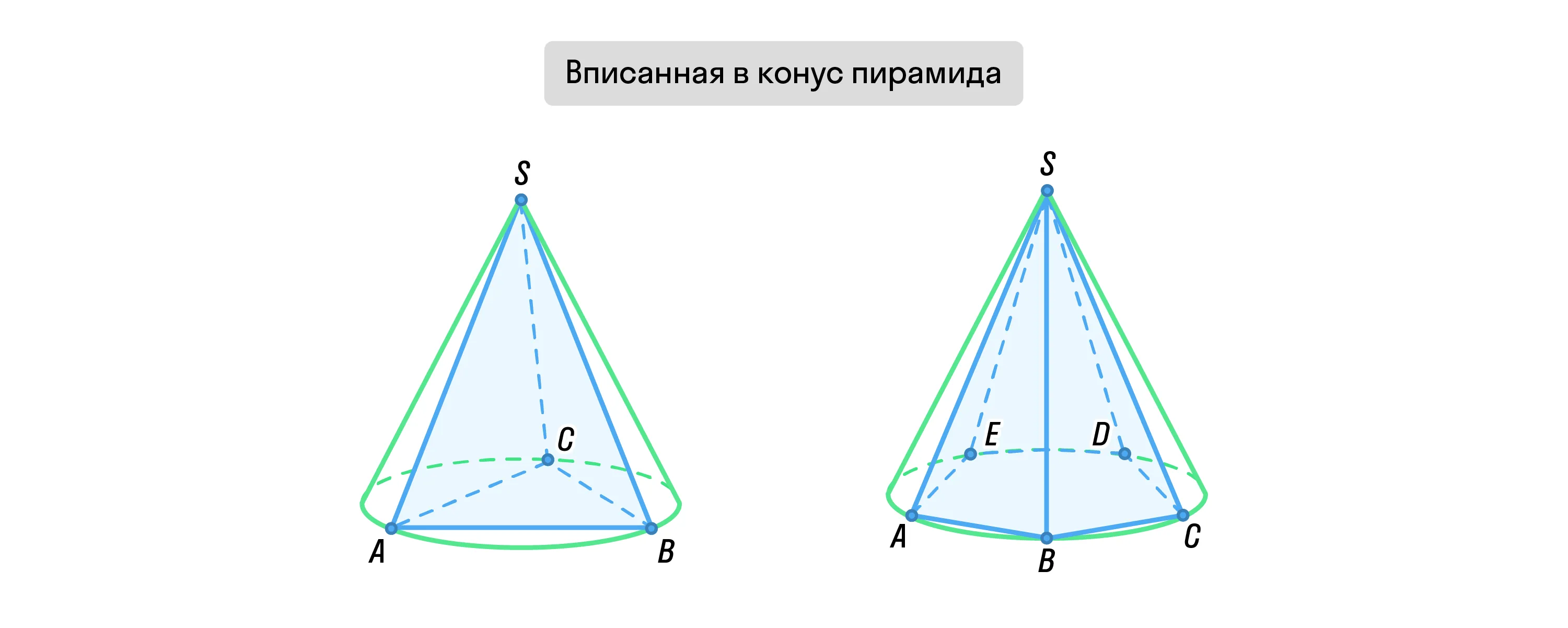
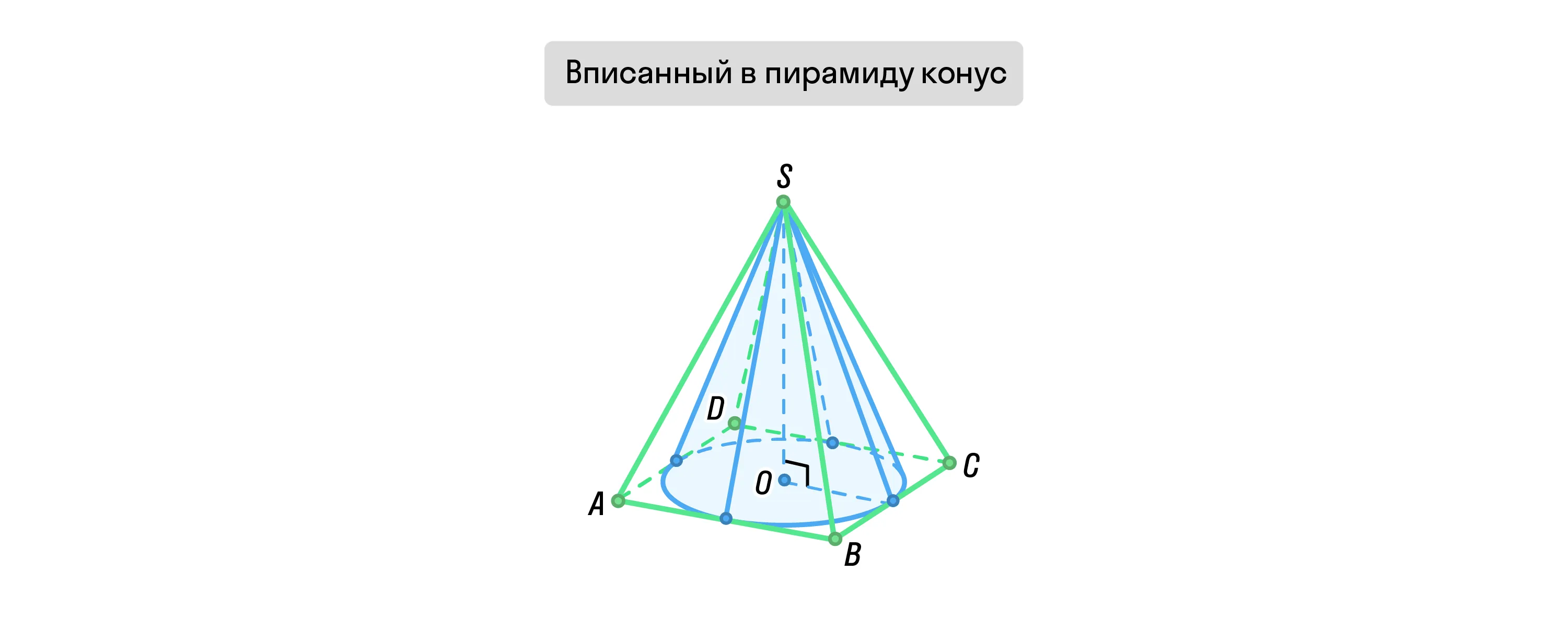
Также конус можно вписать в пирамиду. Но только в том случае, если совпадают их вершины, основание конуса вписано в основание пирамиды, а апофемы этой пирамиды равны между собой.
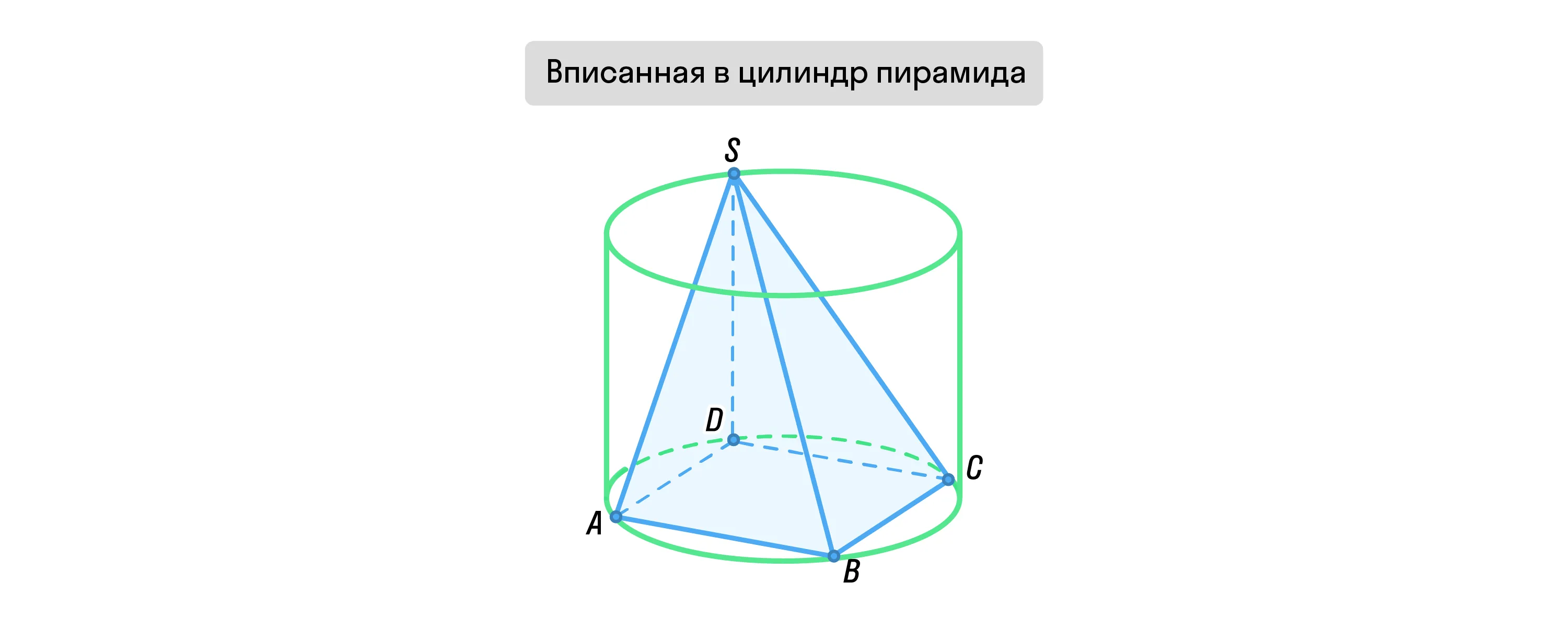
Пирамида и цилиндр
Пирамида называется считается вписанной в цилиндр, если её вершина расположена на одном из оснований цилиндра, а основание самой пирамиды вписано в другое основание цилиндра.
При этом высота вписанной пирамиды равна высоте цилиндра.
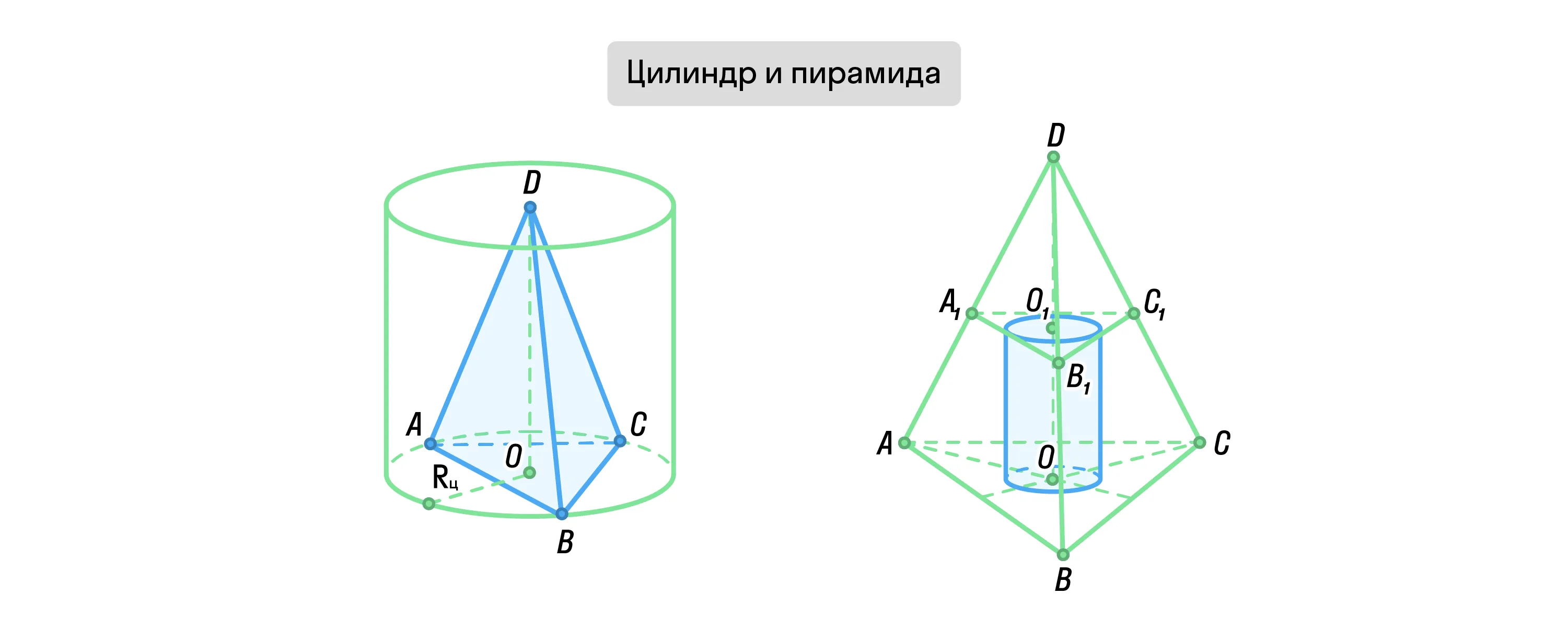
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью, вписанной в сечение пирамиды плоскостью, параллельной основанию. Другое же основание должно быть вписанным в основание пирамиды.
Сечения пирамиды
Если пирамиду пересекает плоскость, параллельная её основанию, то и самое сечение будет подобно многоугольнику, который лежит в этом основании.
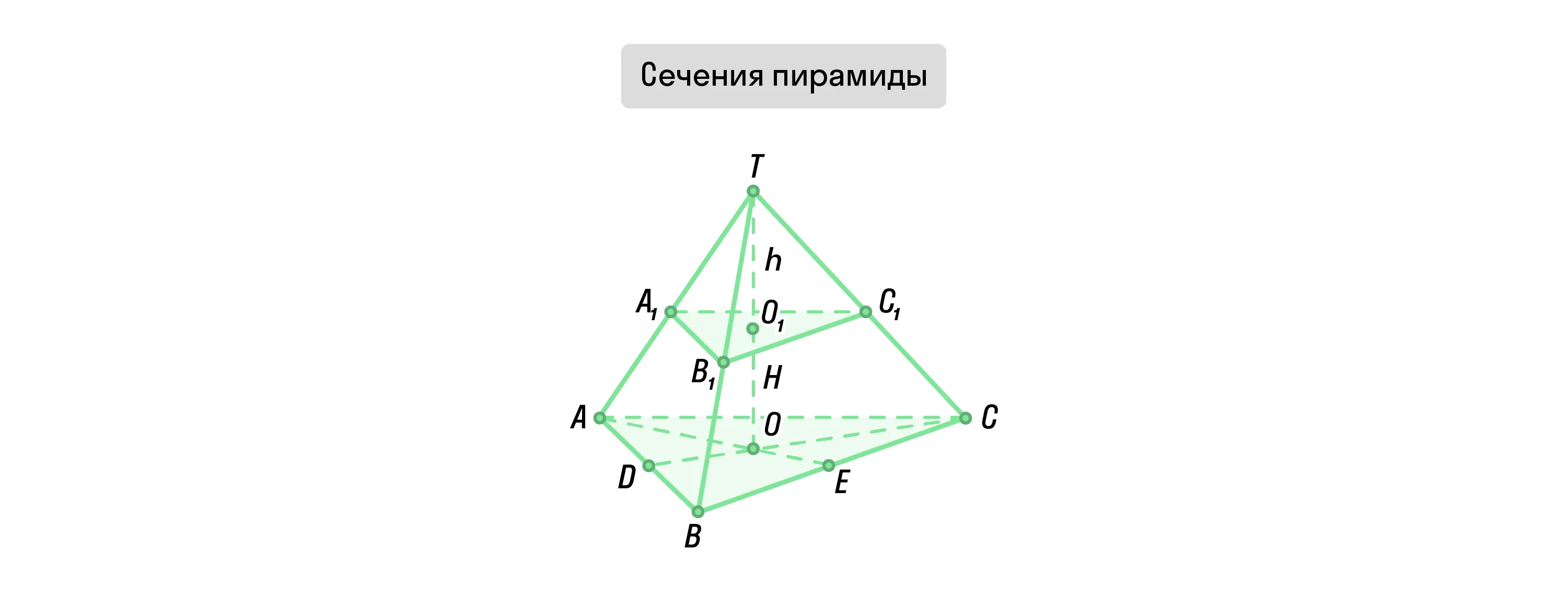
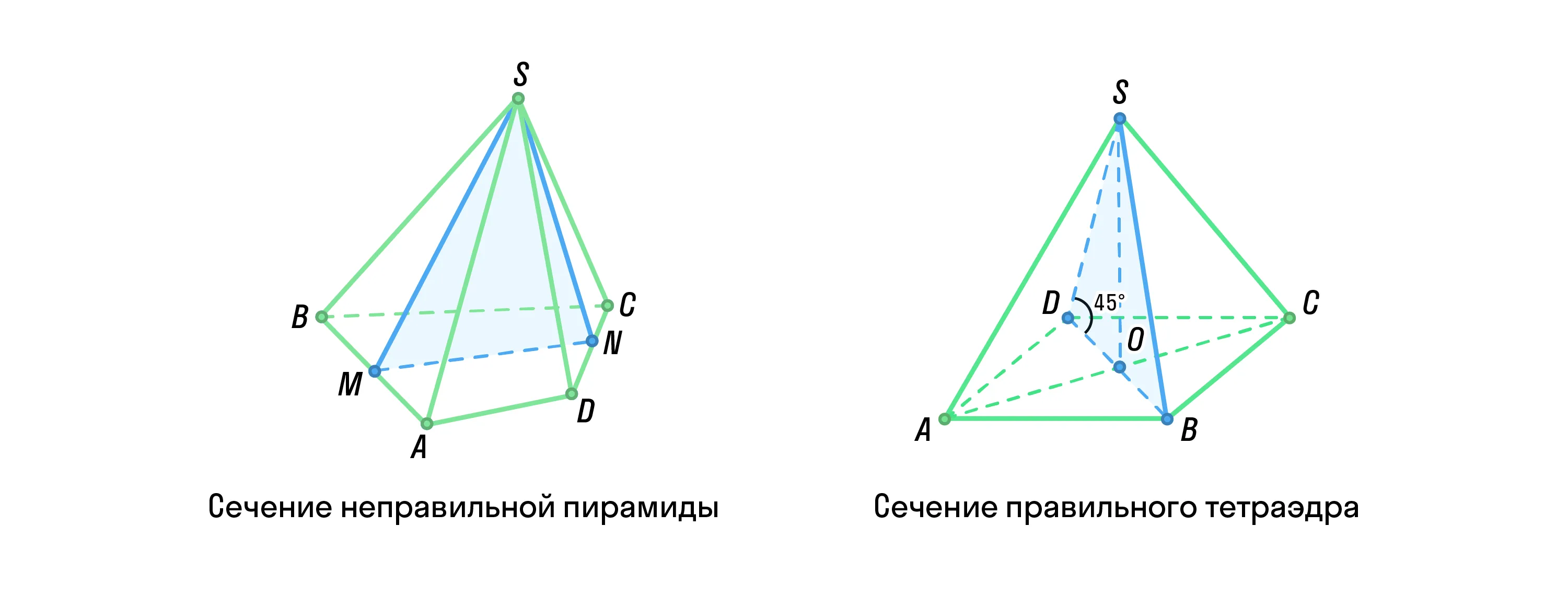
Если пирамиду пересекает плоскость, которая проходит через вершину фигуры по её высоте и перпендикулярна основанию, сечение будет треугольником. В случае с правильной пирамидой — равнобедренным, а с правильным тетраэдром — равносторонним.
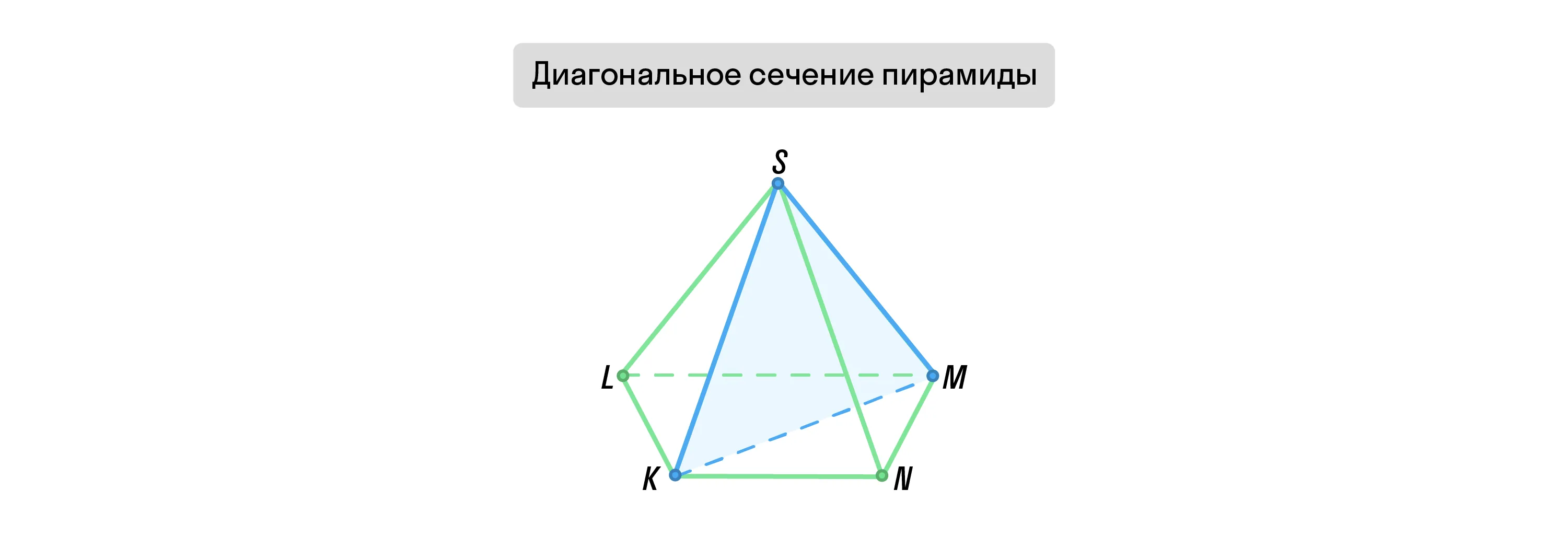
Если пирамиду пересекает плоскость, которая проходит через вершину фигуры и диагональ её основания, это сечение также будет треугольником. Такие сечения называют диагональными.
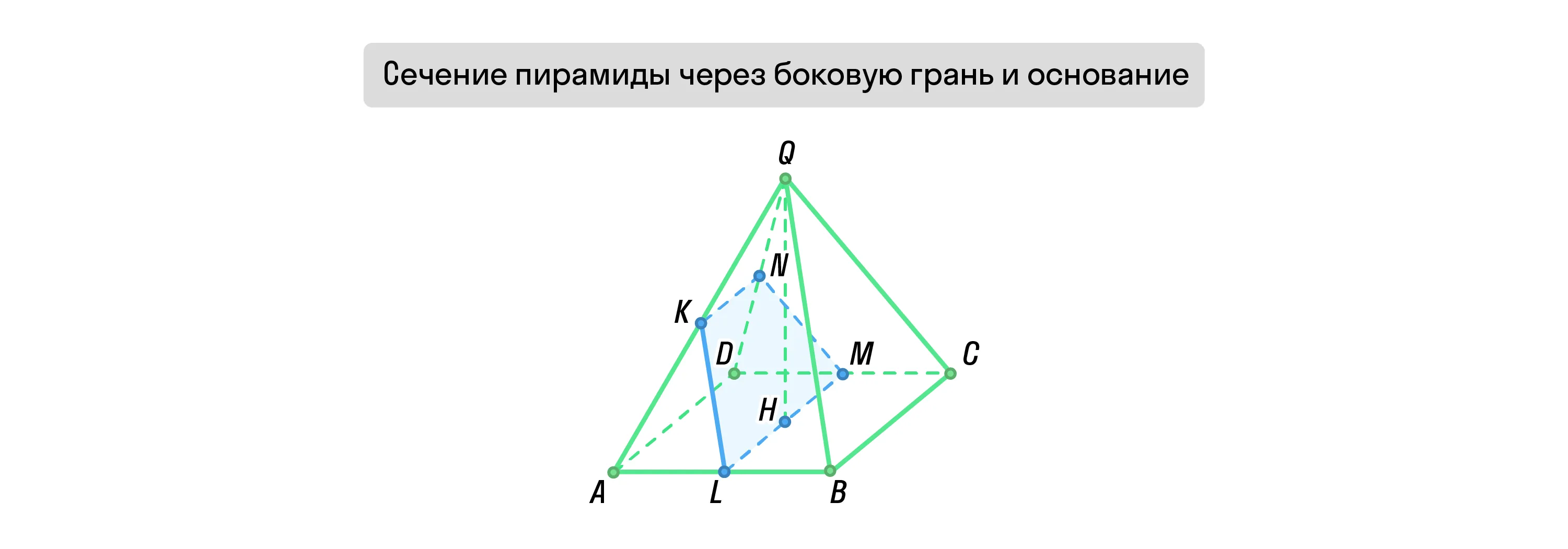
Если пирамиду пересекает плоскость, которая проходит через одну из её боковых граней и основание, такое сечение будет трапецией. В случае с правильной пирамидой трапеция будет равнобедренной.
Все формулы для решения задач с пирамидами
|
Пирамида: все формулы |
|
|---|---|
|
Объём пирамиды через площадь основания и высоту |
|
|
Площадь боковой поверхности правильной пирамиды через периметр основания и апофему |
|
|
Площадь полной поверхности пирамиды через площади боковой поверхности и основания |
|
|
Площадь боковой поверхности правильной усечённой пирамиды через периметры оснований и апофему |
|
|
Объём правильной усечённой пирамиды через площади оснований и апофему |
|
|
Радиус сферы, вписанной в правильную пирамиду, через объём пирамиды и площадь её полной поверхности |
|
|
Радиус сферы, описанной около правильной треугольной пирамиды, через высоту пирамиды и длину ребра её основания |
|
|
Радиус сферы, описанной около правильного тетраэдра, через его высоту и длину ребра основания |
|
|
Радиус сферы, описанной около правильной четырёхугольной пирамиды, через высоту пирамиды и длину ребра её основания |
|
|
Радиус сферы, описанной около правильной шестиугольной пирамиды, через высоту пирамиды и длину ребра её основания |
Узнайте, хорошо ли вы усвоили тему и можете решать экзаменационные задания с помощью Тренажёра ЕГЭ. Это сборник всех типов заданий с автопроверкой ответов, доступный бесплатно 24/7. В нём можно отточить решение задач по одной проблемной теме или написать полноценный пробный экзамен по математике.
В быстро меняющемся мире математика остаётся неизменным основанием, и понимание её фундаментальных элементов, таких как геометрические фигуры, играет важную роль в образовании. Среди самых увлекательных и многогранных форм — пирамида. Этот раздел поможет школьникам разобраться, что такое пирамида в геометрии, изучить её элементы, виды и основные формулы.
Определение пирамиды
Пирамида — это многогранник, который формируется, когда несколько треугольников, сходящихся в одной точке (вершине), соединяются с многоугольником на плоскости (основанием). Эта уникальная структура делает пирамиду одним из наиболее интересных объектов в геометрии (рис. 1).
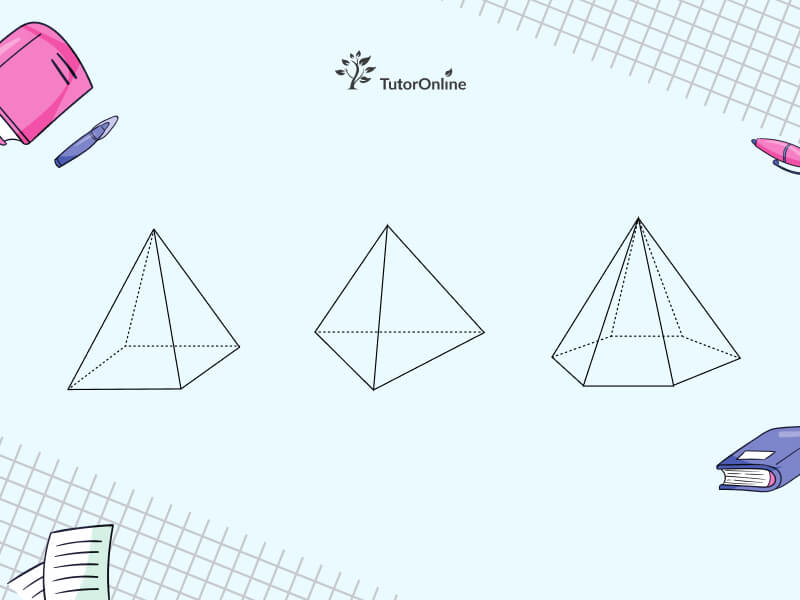
Рисунок 1 — Пирамида
Элементы пирамиды
Пирамида, как геометрическое тело, состоит из нескольких ключевых элементов (рис. 2), каждый из которых имеет свою уникальную роль в структуре и свойствах фигуры.
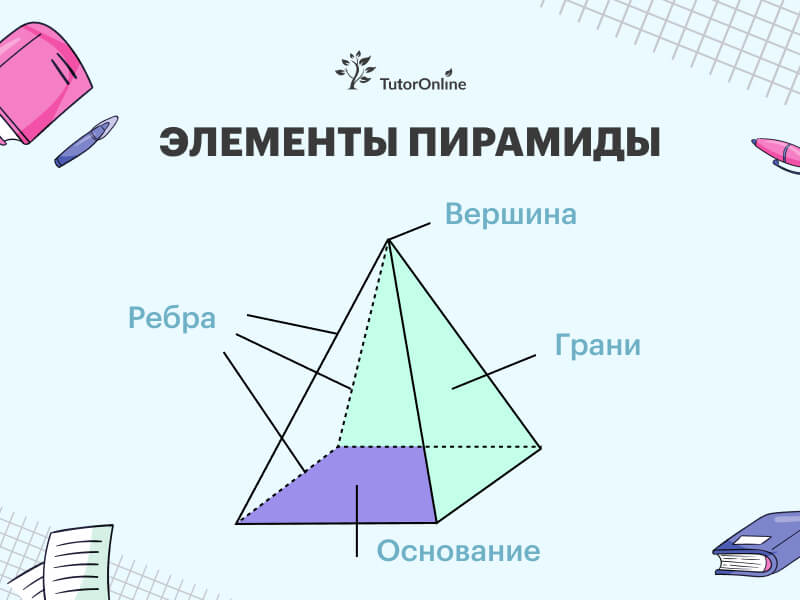
Рисунок 2 — Элементы пирамиды
Вершина пирамиды
Вершина пирамиды — это точка, к которой сходятся все боковые грани. В геометрическом смысле вершина является точкой пересечения прямых, которые образуют рёбра. В зависимости от типа пирамиды, вершина может располагаться прямо над центром основания или смещена относительно него, что создаёт различные виды асимметрии и дает пирамиде уникальные свойства.
Основание пирамиды
Основание пирамиды — это многоугольник, находящийся в основе фигуры. Этот многоугольник может быть любым — от треугольника до многоугольника с большим количеством сторон. В зависимости от формы основания пирамиды могут быть разделены на разные типы, например, тетраэдр имеет треугольное основание, а правильная четырёхугольная пирамида — квадратное или прямоугольное.
Грани пирамиды
Кроме основания, пирамида имеет боковые грани, каждая из которых представляет собой треугольник. Эти треугольники соединяются одной вершиной, которая, как было сказано выше, называется вершиной пирамиды. Боковые грани важны для определения многих свойств пирамиды, включая площадь боковой поверхности и объем.
Рёбра пирамиды
Рёбра пирамиды — это отрезки, которые соединяют вершины многоугольника основания с вершиной пирамиды или друг с другом вдоль основания. В пирамиде выделяют основания рёбер и боковые рёбра. Боковые рёбра играют ключевую роль в формировании углов наклона боковых граней и определении формы пирамиды.
Высота пирамиды
Высота пирамиды — это перпендикуляр, опущенный из вершины на плоскость основания. Высота является ключевым элементом в расчётах объема пирамиды. В пирамидах с регулярным многоугольником в основании высота также помогает определить центр тяжести, что важно в архитектуре и инженерии.
Каждый из этих элементов важен не только для понимания структуры пирамиды, но и для применения геометрических знаний в практических задачах, таких как архитектурное проектирование, конструирование и математическое моделирование.
Развертка пирамиды
Развертка пирамиды — это способ представления всех её боковых граней и основания на одной плоскости (рис. 3). Это полезно для изучения свойств фигуры и для выполнения различных практических заданий, например, в моделировании.

Рисунок 3 — Развертка пирамиды
Основные формулы пирамиды: объем и площадь
Формула площади полной поверхности пирамиды
Для расчета полной площади поверхности пирамиды необходимо сложить площади всех боковых граней и площадь основания:
Sполн = Sбок + Sосн.
Формула площади боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды можно найти, используя длину апофемы (высота боковой грани — h) и периметр основания:
Sбок = 1/2 · Pосн · h.
Формула объема пирамиды
Объем пирамиды определяется как одна треть произведения площади основания на высоту:
V = 1/3 · Sосн · Н.
Виды пирамид
Правильная пирамида
Правильная пирамида имеет равные стороны в основании и равнонаклонные боковые грани (рис. 4).
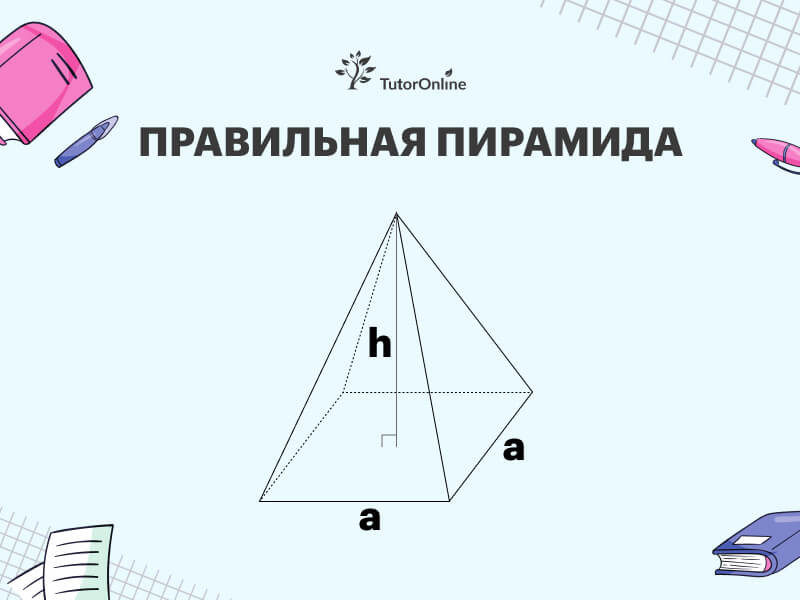
Рисунок 4 — Развертка пирамиды
Теорема о площади боковой поверхности правильной пирамиды
Теорема о площади боковой поверхности правильной пирамиды представляет собой ключевой аспект в изучении геометрии многогранников, особенно тех, у которых основание — правильный многоугольник.
Для правильной пирамиды площадь боковой поверхности (S) может быть вычислена по формуле:
S = 1/2 · P · l,
где P — периметр основания пирамиды, а l — апофема, то есть высота боковой грани пирамиды.
Апофема (l) — это расстояние от центра основания до середины любой из боковых граней. Это перпендикуляр, опущенный из вершины боковой грани (не вершины пирамиды) к середине стороны основания, который лежит у основания этой грани.
Причина, по которой используется именно апофема, заключается в том, что каждая боковая грань правильной пирамиды является равнобедренным треугольником. Высота этого треугольника, или апофема, является определяющим фактором для расчёта площади одной грани.
Таким образом, чтобы найти площадь боковой поверхности правильной пирамиды, можно умножить периметр основания на апофему и на 0.5 (поскольку площадь треугольника вычисляется как 0.5 × основание × высоту).
Пирамида с боковым ребром, перпендикулярным основанию
Эта форма пирамиды характеризуется особым расположением боковых рёбер, образующих прямой угол с плоскостью основания.
Усеченная пирамида
Усеченная пирамида получается в результате среза вершины пирамиды параллельно основанию, что формирует новое основание сверху (рис. 5).
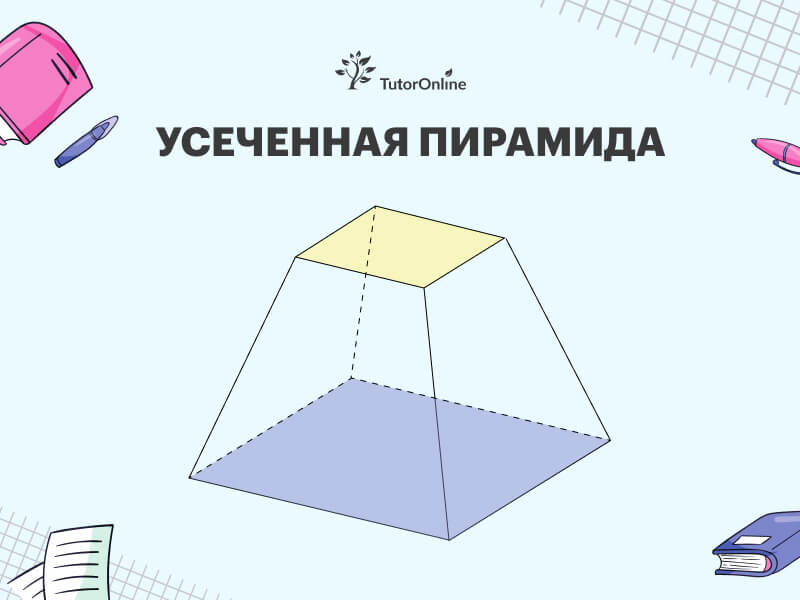
Рисунок 5 — Усеченная пирамида
Примечание: в отдельной статье представлены задачи на усеченную пирамиду.
Теорема о площади боковой поверхности усечённой пирамиды
Теорема определяет, как можно вычислить площадь боковой поверхности этого многогранника, который получается путём среза верхушки пирамиды плоскостью, параллельной основанию.
Формулировка теоремы
Площадь боковой поверхности усеченной пирамиды можно найти по следующей формуле:
S = 1/2 · (P + P′) · l,
где:
- P — периметр нижнего (большего) основания усеченной пирамиды,
- P′ — периметр верхнего (меньшего) основания,
- l — апофема усеченной пирамиды, то есть высота боковой грани, проведенная перпендикулярно к линии, соединяющей основания.
Объяснение:
Апофема усеченной пирамиды играет ту же роль, что и апофема обычной пирамиды, только она проводится между двумя параллельными основаниями и является высотой трапеции, которой является каждая боковая грань усеченной пирамиды. Благодаря параллельности оснований, все боковые грани усеченной пирамиды представляют собой трапеции, что отличает их от треугольных боковых граней полной пирамиды.
Сумма периметров двух оснований учитывается, потому что боковая поверхность усеченной пирамиды складывается из площадей трапеций, основания которых равны периметрам верхнего и нижнего оснований пирамиды.
Тетраэдр
Тетраэдр — это частный случай пирамиды, основанием которого является треугольник.
Свойства пирамиды
Пирамиды обладают уникальными свойствами, включая свойства симметрии, равенства углов и пропорциональности элементов в зависимости от типа пирамиды. Изучение этих свойств помогает глубже понять геометрические взаимосвязи и принципы.
Пирамиды не только красивы и интригующи визуально, но и являются важным элементом в изучении геометрии. Они находят применение в различных областях, от архитектуры до астрономии, что делает их важной темой для школьного образования. В этой статье мы рассмотрели основные аспекты пирамид, которые помогут учащимся лучше понять эту фасцинирующую геометрическую фигуру.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Загрузить PDF
Загрузить PDF
Модель пирамиды довольно легко создать, если у вас есть подходящие материалы и вы знаете, как их правильно измерить, разрезать и склеить. Можно сделать простую пирамиду из картона или бумаги. Для этого аккуратно измерьте и вырежьте стороны пирамиды, а затем соедините их клеем или скотчем. Можно также соорудить ступенчатую пирамиду из кубиков сахара и клея. Какой бы материал вы ни выбрали, изготовление пирамиды является простым и увлекательным способом выполнить школьный проект с помощью доступных подручных средств.
-
Используйте карандаш и линейку, чтобы нарисовать квадрат на чистом листе бумаги. Возьмите линейку в свою неведущую руку и проведите вдоль нее карандашом прямые стороны квадрата.[1]
- Чтобы у вас получилась масштабная модель пирамиды Хеопса, нарисуйте квадрат со стороной 7,7 сантиметра. При этом каждый сантиметр будет соответствовать 30 метрам пирамиды.
-
С помощью линейки определите середину одной стороны квадрата и отметьте ее точкой. Затем разверните линейку и проведите от точки перпендикулярную к стороне линию. Проделайте это для всех сторон квадрата.[2]
- Для масштабной модели пирамиды Хеопса следует поставить точку на расстоянии 3,85 сантиметра от угла каждой стороны и провести от нее перпендикулярный прямой отрезок длиной 6,2 сантиметра.
- Если вы не ставили целью сделать модель пирамиды Хеопса, можно просто провести достаточно длинные линии для того, чтобы они доставали до других граней в центре пирамиды, когда вы согнете их. Для уверенности сделайте каждую линию хотя бы такой же длины, что и сторона квадрата.
-
Соедините каждую линию карандашом с двумя ближайшими к ней углами квадрата. Приложите линейку к верхнему концу линии и соедините его с ближайшим левым углом квадрата. Затем проведите симметричную линию к правому углу квадрата. Проделайте это для всех четырех линий — в результате у вас получится 8 прямых отрезков, которые соединяют внешние концы линий с соответствующими углами квадрата.[3]
- Таким образом, у вас получится 4 треугольника, основания которых совпадают со сторонами квадрата.
- Для соблюдения масштаба длина каждой соединительной линии должна составлять 7,3 сантиметра.
-
Возьмите лист бумаги своей неведущей рукой и разрежьте его ножницами вдоль внешних краев линий. Продолжайте до тех пор, пока полностью не вырежете из бумаги весь рисунок. В результате у вас получится один разрез вдоль всего края пирамиды.[4]
Совет: чтобы легче разрезать бумагу в острых углах, вращайте ее, а не поворачивайте ножницы.
-
Положите вырезанную фигуру на ровную поверхность. Своей неведущей рукой сделайте складку вдоль каждой стороны квадрата, а затем согните все треугольники к центру. Пройдитесь вдоль каждой складки кончиками пальцев. Загните каждую боковую сторону к центру квадрата.[5]
- Можно согнуть каждую боковую грань так, чтобы она легла на квадрат, а затем разогнуть, и по очереди проделать это со всеми боковыми сторонами, чтобы они не мешали друг другу. Так вам будет намного легче.
-
Закрепите края граней пирамиды скотчем там, где они стыкуются друг с другом. Подтяните загнутые треугольники к центру, чтобы их края коснулись друг друга, и закрепите их вдоль линий соединения прозрачным скотчем. Наложите длинные полоски скотча вдоль каждой линии стыка треугольников, после чего слегка прижмите их по бокам.[6]
- Прижимайте скотч медленно и аккуратно. Не забывайте, что внутри пирамиды пусто, поэтому действуйте осторожно, чтобы не разрушить ее.
-
Покройте пирамиду клеем, чтобы добавить песок, если вы хотите, чтобы она выглядела более реалистично. Поставьте пирамиду в небольшой пластиковый контейнер для бутербродов или на бумажную тарелку, чтобы не рассыпать песок. Возьмите кисточку для краски и нанесите белый клей на каждую грань пирамиды. Не жалейте клея и смочите им всю видимую поверхность пирамиды.[7]
- Покройте клеем все стороны пирамиды, но при этом следите, чтобы на них не осталось крупных комков. Под их весом бумага может прогнуться, и пирамида сломается.
-
Не спеша насыпьте песок на верхнюю часть пирамиды, чтобы он покрыл все боковые грани. Подбирайте упавший на дно контейнера песок ложкой и вновь посыпайте им пирамиду. Продолжайте до тех пор, пока не покроете ее песком полностью. После этого подождите 45–60 минут, чтобы пирамида высохла.[8]
Реклама
-
Чтобы пирамида имела правильную форму, треугольники должны быть одинакового размера. Сначала отмерьте основание треугольника, а затем проведите из его центра перпендикуляр. После этого с помощью линейки соедините прямыми линиями вершину каждого перпендикуляра с обоими концами основания.[9]
- Чтобы сделать пирамиду средних размеров, нарисуйте треугольники с длиной основания 20 сантиметров и высотой 30 сантиметров.
-
Положите лист картона на устойчивую поверхность и придерживайте его своей неведущей рукой. В преобладающую руку возьмите ножницы или нож и вырежьте треугольники вдоль сторон. В результате у вас получится 4 одинаковых треугольника.[10]
- Если картон слишком толстый, чтобы разрезать его ножницами, положите его на разделочную доску и вырежьте каждый треугольник вдоль сторон универсальным ножом.
-
Включите клеевой пистолет, положите рядом с собой и подождите, пока нагреется клей. Возьмите двумя руками два треугольника, прижмите их основания к рабочей поверхности и соедините боковыми сторонами. Удерживайте треугольники в таком положении своей неведущей рукой, а в преобладающую руку возьмите клеевой пистолет. Нажмите спусковой крючок на пистолете и нанесите клей вдоль соединенных вместе краев треугольников.[11]
- Продолжайте удерживать треугольники в первоначальном положении 45–60 секунд, чтобы клей подсох. Затем отставьте их в сторону на 10–20 минут, чтобы клей полностью высох.
-
Таким же образом соедините два других треугольника, нанесите вдоль линии стыка клей и подождите, пока он высохнет. Затем расположите обе половины пирамиды на ровной поверхности так, чтобы соединить их свободные края. В результате у вас сложится пока что не склеенная пирамида. Нанесите горячий клей на два оставшихся стыка и подождите 10–20 минут, пока он высохнет.[12]
- После того как вы нанесете клей на два оставшихся края, слегка прижмите половинки пирамиды друг к другу на 30–45 секунд, чтобы между ними не осталось зазоров, пока клей подсыхает.
-
Основание можно отмерить так, чтобы оно идеально прилегало к боковым сторонам пирамиды и удерживало склеенные треугольники вместе — в этом случае длина стороны основания должна равняться длине основания каждого треугольника. Можно также определить необходимые размеры основания и сделать его немного больше, чтобы оно выступало на одинаковое расстояние со всех сторон. Начертите основание с помощью треугольной линейки и карандаша и вырежьте его ножницами или универсальным ножом.[13]
- Для пирамиды среднего размера подойдет основание 36×36 сантиметров.
-
Проведите водостойким маркером вертикальные и горизонтальные линии, чтобы изобразить каменные блоки. Чтобы казалось, что пирамида сложена из отдельных каменных блоков, нарисуйте на каждой боковой грани параллельные горизонтальные линии черным маркером. Эти линии не обязательно должны быть идеально прямыми, если вы хотите, чтобы они выглядели естественно, хотя при желании можно сделать их достаточно ровными. Нанесите вертикальные отрезки между каждым горизонтальным рядом на расстоянии 2,5–5 сантиметров друг от друга, чтобы изобразить отдельные каменные блоки.[14]
Совет: линии будут лишь частично видны после того, как вы покроете пирамиду клеем и песком, поэтому не беспокойтесь, если допустите ошибку.
-
Нанесите на каждую грань клей с помощью ножа для масла или палочки от мороженого. Налейте на пирамиду немного белого клея и размажьте его палочкой от мороженого или ножом для масла. Покройте клеем почти всю поверхность пирамиды.[15]
- Не забудьте об основании! Как следует смажьте клеем боковые стороны возле основания пирамиды, чтобы песок полностью покрывал их.
-
Пока клей не высох, посыпьте всю поверхность пирамиды песком. Не спеша рассыпьте песок в 10–15 сантиметрах над каждой стороной и дайте ему собраться у основания, чтобы пирамида имела естественный вид. После этого подождите 1–2 часа, пока пирамида высохнет, прежде чем прикасаться к ней.[16]
- Если вы хотите, чтобы каменные блоки лучше проступали сквозь песок, его можно стряхнуть в некоторых местах ножом или палочкой от мороженого.
Реклама
-
Нанесите на тарелку белый клей. Ровным слоем размажьте его кисточкой для клея в том месте, где вы собираетесь возвести пирамиду. Это послужит ее основанием, поэтому проследите, чтобы клей покрывал всю поверхность.[17]
- В качестве основания пирамиды можно использовать также пластиковый поднос или доску.
- Для пирамиды с основанием 7×7 вам понадобится 140 кубиков сахара.
-
Начните с угла пирамиды. Окуните первый кубик в клей и слегка прижмите его к нужному месту. Продолжайте выкладывать кубики в обоих направлениях, пока у вас не получится две перпендикулярные стороны длиной по 7 кубиков. После этого заполните кубиками сахара оставшееся место, чтобы вышел квадрат 7×7.[18]
Совет: не прижимайте кубики первого слоя к основанию слишком сильно, иначе они могут рассыпаться. Вам не понадобится много усилий, чтобы приклеить кубики сахара, так как они пористые.
-
Нанесите клей на нижний слой кубиков, так чтобы смазать им квадрат 6×6 посередине. По зазорам между кубиками первого слоя определите, где будет находиться второй квадрат 6×6 кубиков. Смажьте клеем края этого квадрата, а затем его середину. Нанесите хотя бы одну достаточно большую каплю клея на каждый внутренний кубик, чтобы как следует закрепить верхний слой.[19]
-
Пока клей не высох, нанесите на нижние кубики второй слой из 6×6 кубиков. Положите каждый верхний кубик прямо на нижний слой. При этом не надавливайте на кубики.[20]
- Чтобы сэкономить время, выложите верхний слой кубиков на отдельную тарелку и переносите их целыми рядами, сжимая двумя пальцами.
-
Выкладывайте следующие слои так, чтобы сторона квадрата была на один кубик короче предыдущего слоя. Выложите слой из 5×5, затем из 4×4 кубиков, и так далее. Каждый раз добавляйте клей, прежде чем положить следующий слой.[21]
- Выкладывайте кубики ровными постепенно уменьшающимися квадратами, иначе пирамида может развалиться.
- При желании можно покрыть пирамиду клеем, блестками, песком или краской.
Реклама
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Ножницы
- Скотч
- Клей
- Небольшой контейнер для бутербродов
- Песок
- Лист картона
- Карандаш
- Линейка
- Ножницы или универсальный нож
- Клеевой пистолет
- Клеевые палочки
- Водостойкий маркер
- Клей
- Нож для масла или палочка от мороженого
- Песок
- Бумажная тарелка
- Кубики сахара
- Клей
- Блестки, краска или песок (по желанию)
Об этой статье
Эту страницу просматривали 75 238 раз.
Была ли эта статья полезной?
Многогранник, одна грань которого является \(n\)-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, \(n\)-угольник называется основанием пирамиды, а треугольники — боковыми гранями.
Общая вершина боковых граней называется вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок:
1) первым рисуется основание,
2) по условию задачи находится проекция вершины на плоскости основания,
3) вертикально проводится высота,
4) проводятся рёбра.
На рисунке изображена четырёхугольная пирамида \(SABCD\)
(первой пишут букву вершины).
Основание — четырёхугольник \(ABCD\).
Вершина проецируется в точку пересечения диагоналей \(O\) — основание высоты или проекция вершины.
\(SA\), \(SB\), \(SC\), \(SD\) — рёбра пирамиды,
\(AB\), \(BC\), \(CD\), \(DA\) — стороны основания.
В курсе средней школы в основном есть задачи, в которых даны:
— правильная пирамида (вершина проецируется в центр основания);
— пирамида, вершина которой проецируется в центр описанной окружности;
— пирамида, вершина которой проецируется в центр вписанной окружности;
— пирамида, высота которой совпадает с боковым ребром;
— пирамида, высота которой также является высотой боковой грани.
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды.
Двугранный угол между боковой гранью \(SCD\) и гранью основания равен линейному углу
∠
\(OES\). Этот угол образован отрезками \(OE\) и \(SE\), лежащими в этих гранях и перпендикулярных их общей прямой \(CD\). То есть \(OE\)
⊥CD
и \(SE\)
⊥CD
.
Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах.
Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания.
На рисунке
∠
\(OCS\).
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды.
Основные формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды:
S=S1+S2+S3+…
(Некоторые формулы годятся только для определённых видов пирамиды.)
Площадь полной поверхности
Sп.п.=S+Sоснования
.
Объём пирамиды \(V =\)
13Sоснования
\(H\), где \(H\) — высота пирамиды.
Формула объёма используется для пирамид любого вида.
Источники:
Рис. 1. Пирамида, © ЯКласс.
План урока:
Понятие пирамиды
Правильная пирамида
Усеченная пирамида
Типичные задачи на пирамиды
Понятие пирамиды
Построим на некоторой плос-ти α произвольный многоугольник А1А2…Аn. Далее отметим в пространстве точку Р, не принадлежащую плос-ти α. Соединив точку Р с вершинами многоуг-ка получим многогранник, который именуется пирамидой (в различной литературе может использоваться сокращение пирам-а).

Та единственная точка Р, не находящаяся в одной плос-ти со всеми остальными вершинами, именуется вершиной пирам-ы. Многоугольник, образованный остальными вершинами – это основание пирамиды.

Основанием пирам-ы может быть многоугольник с любым количеством сторон. Если в основании лежит, например, пятиугольник, то и пирам-у называют пятиугольной. Если же в основании находится десятиугольник, то это будет уже десятиугольная пирам-а. В общем случае пирам-у, у которой в основании располагается n-угольник, именуется n-угольной. Ясно, что треугольная пирам-а и тетраэдр – это по сути одна и та же фигура.
Все грани пирам-ы, за исключением ее основания, именуются боковыми гранями. Понятно, что каждая боковая грань – это треугольник. Ребра пирамиды, выходящие из ее вершины, именуются боковыми ребрами пирамиды.
Посчитаем количество ребер, вершин и граней пирам-ы. Если она n-угольная, то у неё (n + 1) вершин (n точек в основании и ещё одна точка, не лежащая в основании). Также у нее (n + 1) граней, из них одна – это основание, а остальные n – боковые грани пирамиды (по одной на каждую сторону n-угольника). Наконец, у пирам-ы n ребер находятся в плос-ти основания, а ещё n ребер являются боковыми. Итого имеем 2n ребер. Теперь можно убедиться, что теорема Эйлера для пирам-ы выполняется:
Из вершины пирам-ы можно опустить перпендикуляр на плос-ть основания. Он будет именоваться высотой пирамиды.

Как и в случае с призмой, можно подсчитать площадь боковой поверхности призмы, которую обозначают как Sбок. Если же к ней ещё добавить и площадь основания (Sосн), то в сумме получится уже площадь полной поверхности призмы (Sполн). Эту связь между величинами можно представить в виде формулы:
Правильная пирамида
Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:
1) в их основании находится правильный многоугольник;
2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.
Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.

Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:

Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.
Построим из О радиусы ОА1, ОА2, ОА3,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА1, ∆РОА2, ∆РОА3… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА1, ОА2, ОА3… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА1, РА2, РА3…, также одинаковы, ч. т. д.
Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА1, РА2, РА2… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А1, А2, А3… Получатся прямоугольные ∆РОА1, ∆РОА2, ∆РОА3… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА1, ОА2, ОА3… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА1, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.

Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.

Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.
Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.
Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:

Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:
Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:

Усечённая пирамида
Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА1, РА2, РА3… в точках В1, В2, В3… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.

У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.
Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:
Нам надо доказать, что А1А2В2В1 – это трапеция. Действительно, прямые А1А2 и В1В2 не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А1А2||В1B2. Две другие стороны грани, А1В1 и А2В2, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А1А2В2В1 будет трапецией, ведь у него две стороны параллельны, а две другие – нет.
Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:

Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А1А2А3…An и В1В2В3…Bn:

Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:
Мы уже знаем, что грани А1А2В2В1 и А2А3В3В2 – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.
Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А1А2А3 = ∠В1В2В3. Действительно, мы знаем, что А1А2||В1В2 и А2А3||B2B3, и потому стороны углов ∠А1А2А3 = ∠В1В2В3 оказываются сонаправленными лучами.
Так как в нижнем многоуг-ке А1А2А3…An все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В1В2В3…Bn также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.

Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА1А2А3…Рn была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В1В2В3…Вn– правильный многоуг-к. Отрезки РА1, РА2, РА3… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А1В1, А2В2, А3В3 одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ1, РВ2, РВ3… Значит, в пирам-е РВ1В2В3…Вn в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.
Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:

Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:
Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:

Типичные задачи на пирамиды
Рассмотрим несколько задач, в которых фигурируют пирам-ы. Перед просмотром решения попытайтесь решить их самостоятельно.
Задание. Существует ли пирамида, у которой ровно 999 ребер?
Решение. Если в основании пирам-ы находится n-угольник, то у нее 2n ребер. Так как n– целое число, то 2n будет уже четным числом. То есть количество ребер у любой пирам-ы всегда четно. Поэтому не существует пирам-ы с 999 ребрами, ведь 999 – нечетное число.
Задание. Верно ли, что всякий правильный тетраэдр одновременно является и правильной пирам-ой? И наоборот, является ли каждая правильная треугольная пирам-а правильным тетраэдром?
Решение. Напомним, что правильный тетраэдр – это тетраэдр, у которого все ребра одинаковы. Если одну из вершин тетраэдра принять за вершину пирам-ы, то получится, что в ее основании равносторонний треугольник, который, как мы знаем, является правильным многоуг-ком. Также окажется, что все боковые ребра пирам-ы также одинаковы. Это значит, что она – правильная.
Теперь посмотрим на произвольную правильную треугольную пирам-у. Будет ли она обязательно правильным тетраэдром? Нет, ведь ее боковые ребра могут отличаться по длине от ребер, находящихся в основании. Например, в основании может находиться равносторонний треуг-к со стороной 5 см, а боковое ребро правильной пирамиды может иметь длину 10 см. Таким образом, можно считать правильный тетраэдр лишь частным случаем правильной пирам-ы.

Задание. В основании пирам-ы находится ромб со стороной 5 см.Одна из его диагоналей имеет длину 8 см. Высота пирам-ы имеет длину 7 см и проходит через точку, в которой пересекаются диагонали ромба. Вычислите длину боковых ребер.
Решение.
Обозначим ромб в основании как АВСD, а вершину пирам-ы буквой Р. Пусть диагонали пересекаются в точке О, тогда РО – высота. Также пусть диагональ АС равна 8 см. По свойству ромба О будет серединой диагоналей, поэтому

Отрезок OD будет иметь ту же длину 3 см, ведь О – середина BD.
Так как высота РО перпендикулярна всем прямым в плос-ти основания, то ∆АОР, ∆ВОР, ∆СОР, ∆DOP – прямоугольные, и боковые ребра пирам-ы будут гипотенузами этих треугольников. Вычислим АР по теореме Пифагора:
Задание. В основании пирам-ы лежит квадрат, а одно из ее боковых ребер перпендикулярно основанию. Одна из боковых граней образует с плос-тью основания угол в 45°. Длина длиннейшего ребра пирам-ы составляет 12 см. Определите высоту пирам-ы и площадь ее боковой поверхности.
Решение.

Обозначим квадрат, находящийся в основании, как АВСD, а вершину пирам-ы как Р. Пусть ребро PD перпендикулярно основанию. Тогда PD⊥AD и PD⊥CD. Ясно, что PD как раз и является искомой нами высотой пирам-ы.
Теперь надо понять, какие углы в пирам-е составляют 45° и какое ребро равно 12 см. Грани ADP и СDP проходят через перпендикуляр PDк основанию, а потому они перпендикулярны основанию. Значит, угол в 45° с основанием образует либо грань АВР, либо грань СВР.
Заметим, что АВ⊥AD (это смежные стороны квадрата), а AD – это проекция ребра АР на основание. Тогда по теореме о трех перпендикулярах АВ⊥АР. Аналогично из того факта, что ВС⊥СD, вытекает, что ВС⊥СР. Также заметим, что ∆ADP и ∆СDP прямоугольные, имеют общий катет PD и одинаковые катеты AD и CD (это стороны квадрата). Значит, это равные треугольники, и
∠PAD = ∠PCD
Грань АВР пересекается c основанием по прямой АВ, причем AD⊥АВ и АР⊥АВ. Значит, ∠РАD – это угол между гранью АВР и основанием. Аналогично и ∠РСD является углом между гранью СВР и основанием. Но эти углы одинаковы. Значит, каждый из этих углов будет равен 45°, иначе в пирам-е не останется угла между плос-тями, который мог бы составлять 45°.
Ясно, что ребро АР длиннее ребра РD, ведь в прямоугольном ∆ADP АР – это гипотенуза, а РD катет (гипотенуза всегда длиннее катета). Теперь заметим, что ∆РАВ и ∆РСВ – также прямоугольные, ведь АВ⊥АР и ВС⊥СР. Но в них гипотенузой является уже РВ, то есть РВ длиннее АВ, ВС, АР и РС. Так как отрезки AD и AC равны АВ как стороны квадрата, получаем, что именно ребро РВ – длиннейшее в пирам-е, то есть его длина составляет 12 см.
В прямоугольном ∆ADP∠PAD = 45°. Это значит, что ∆ADP является прямоугольным и равнобедренным, то есть AD = PD. Обозначим искомую нами длину РD как x. Теперь проведем диагональ BD:

Её длину можно вычислить из ∆ADB:

Итак, высоту нашли, теперь нужно рассчитать боковую площадь. Но для этого предварительно найдем АР из ∆АРD:
Такую же длину имеет и РС, ведь ∆АРD и ∆СРD равны.
Мы уже выяснили, что каждая боковая грань – прямоугольный треугольник. Зная длины катетов, легко найдем площадь каждой грани:

Задание. В правильной шестиугольной пирам-е ребро при основании равно 3 см. Высота этой пирам-ы составляет 4 см. Вычислите длину апофемы этой пирам-ы, а также угол, который ее боковые грани образуют с основанием.
Решение.

Основание пирам-ы обозначим как АВСDEF, а вершину как Р. Пусть РО – высота, тогда О – центр описанной окружности. Напомним, что у правильного шестиугольника радиус описанной окружности совпадает с длиной его стороны, то есть

Теперь надо найти угол между гранью АВР и основанием. Они пересекаются по прямой АВ. РН⊥АВ, ведь РН – апофема. ОН – это проекция РН на основание. Так как АВ⊥РН, то по обратной теореме о трех перпендикулярах и ОН⊥АВ. Значит, ∠ОНР и является искомым углом между гранью АВР и основанием. Для его вычисления применим тригонометрию к ∆ОНР:
Задание. В правильной шестиугольной пирам-е все ребра имеют длину, равную единице. Найдите угол между прямыми АР и BD:

Решение. Для нахождения угла между АР и BD, у которых нет общей точки, можно вычислить угол между прямыми, которые будут им параллельны. Легко заметить, что АЕ||BD. Докажем это, рассмотрев основание пирам-ы:

Каждый угол правильного шестиугольника составляет 120°. В частности, это относится к ∠F и ∠С. ∆АFЕ – равнобедренный, ведь его стороны FE и AF одинаковы. Тогда и углы при основании будут одинаковыми. Найдем их:

Аналогично можно определить, что все углы четырехугольника АВDE прямые, то он представляет собой прямоугольник. Его противоположные стороны параллельны, в частности, АЕ||BD. Это означает, что искомый нами угол – это ∠РАЕ:

Для его вычисления необходимо вычислить длины сторон ∆РАЕ. Ребра РА и РЕ по условию равны единице. Длину ЕА найдем из ∆FAE, применив теорему косинусов:

Задание. В правильной шестиугольной пирам-е боковые ребра имеют длину 2, а ребра в основании равны 1. Вычислите угол между плос-тями РFA и PDE:

Решение. Сначала надо найти прямую, по которой эти две грани пересекаются. Мы видим одну их общую точку – Р. Продолжим ребра FA и ED до тех пор, пока они не пересекутся в некоторой точке К. Эта точка K также будет общей для плос-тей, проходящих через грани PFA и РЕD. Значит, они пересекаются по прямой РК:

Найдем углы в ∆КЕF, помня при этом, что все в шестиугольнике АВСDEF составляют по 120°:

Получили, что все углы в ∆КЕF составляют по 60°, то есть он равносторонний, и поэтому стороны KE и KF одинаковы. Но также одинаковы и грани FA и DE. Отсюда получаем и равенство отрезков АК и DK:
Теперь сравним ∆АРК и ∆KPD. КР – их общая сторона, АР = РD как боковые ребра правильной пирам-ы, и АК = DK. Получается, что эти треугольники равны.
Далее в ∆АРК опустим высоту АН. Из равенства ∆АРК и ∆KPD вытекает, что и HD будет высотой в ∆PHD, ведь в равных треугольниках высоты должны делить равные стороны в одном и том же отношении. Тогда по определению двугранного угла ∠AHD и будет искомым углом между гранями, ведь KP – линия их пересечения, АН⊥KP и DH⊥KP.

∆AKP – равнобедренный, ведь отрезки АК и АР оказались одинаковыми. Значит, АН не только высота, но и медиана. Поэтому

Отрезок AD окажется диаметром окружности, описанной около шестиугольника. Мы знаем, что радиус такой окружности равен длине стороны шестиугольника, то есть единице. Тогда диаметр будет вдвое больше:

Сегодня мы познакомились с ещё одним видом многогранника –пирамидой. Они нередко встречаются в задачах ЕГЭ, посвященных стереометрии. Особо часто используются правильные пирамиды, поэтому важно помнить их основные свойства.